In this paper, we give a precise and workable definition of a quantum knot system, the states of which are called quantum knots. This definition can be viewed as a blueprint for the construction of an actual physical quantum system. arxiv ![]()
Of course, unlike a classical closed piece of rope, a quantum knot can exhibit non-classical behavior, such as quantum superposition and quantum entanglement. This raises some interesting and puzzling questions about the relation between topological and quantum entanglement.
The knot type of a quantum knot is simply the orbit of the quantum knot under the action of the ambient group. We investigate quantum observables which are invariants of quantum knot type. We also study the Hamiltonians associated with the generators of the ambient group, and briefly look at the quantum tunneling of overcrossings into undercrossings.
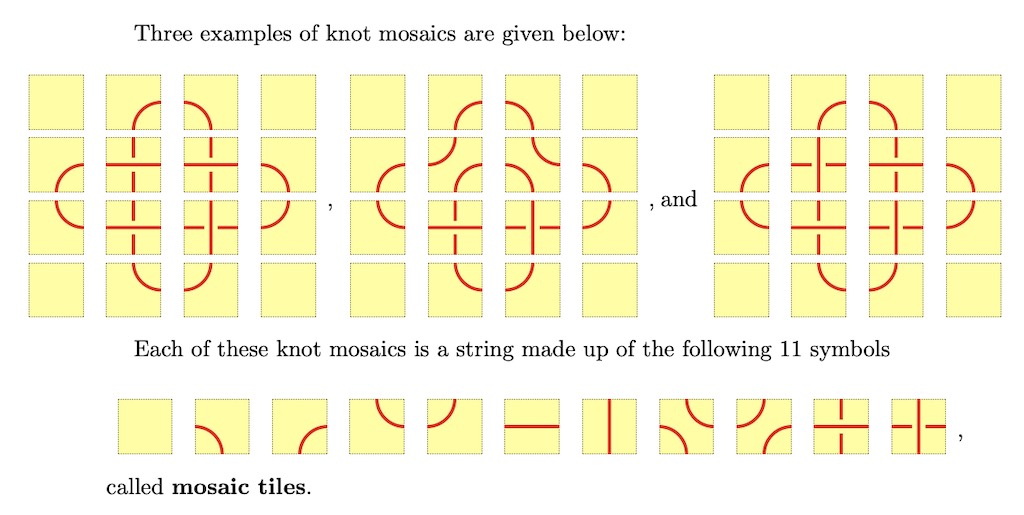
A basic building block in this paper is a mosaic system which is a formal (rewriting) system of symbol strings. We conjecture that this formal system fully captures in an axiomatic way all of the properties of tame knot theory.